字典树的几种实现方式以及应用

29 Aug 2021 | Trie, Algorithm | | ˚C

字典树

字典树(Trie)这一概念有时候会跟基数树(Radix Tree)、前缀树(Prefix Tree)等混用。其中前缀树、字典树是从字符串存储角度的称呼，基数树更多是从数值(多为二进制)角度的称呼，可以看作广义的字典树。以下以字典树来统称字典树和基数树。

关于字典树的介绍，前面的文章有一个直观的介绍，也不多赘述。

功能对比

数据结构	增加	删除	精确查找	极值查找	顺序遍历	前缀遍历	数据约束
哈希表	√	√	√				哈希函数;等于比较
堆	√	√		√			小于比较
平衡树	√	√	√	√	√	√	小于比较
字典树	√	√	√	√	√	√	二进制比较(字符比较)

基础版本字典树的特点：

查询时间只和key长度有关，和树中的节点数量无关
设每个字符长度是s bits，一个key长度是k bits，最多只需要比较k / s个node

不足：

基本只适用于基本数据(整数，字符串、二进制串)
很难像哈希表或者平衡树那样，通过自定义哈希函数或者比较函数来存储自定义类型

字典树的优化方向：

减少内存overhead(减少节点大小、分支数量、节点层数)
缓存友好

常规优化

还是主要参见前面介绍HAT的文章。主要有:

字母表缩减。可以看作基数树换用更小的基数。代价是树的深度变大，速度慢。
使用关联容器。代价是每次索引运算量增大。
压缩字典树。把只有一个分叉的节点，连同其唯一的孩子，结合成一个节点。可以通过插入过程中分裂节点来实现：

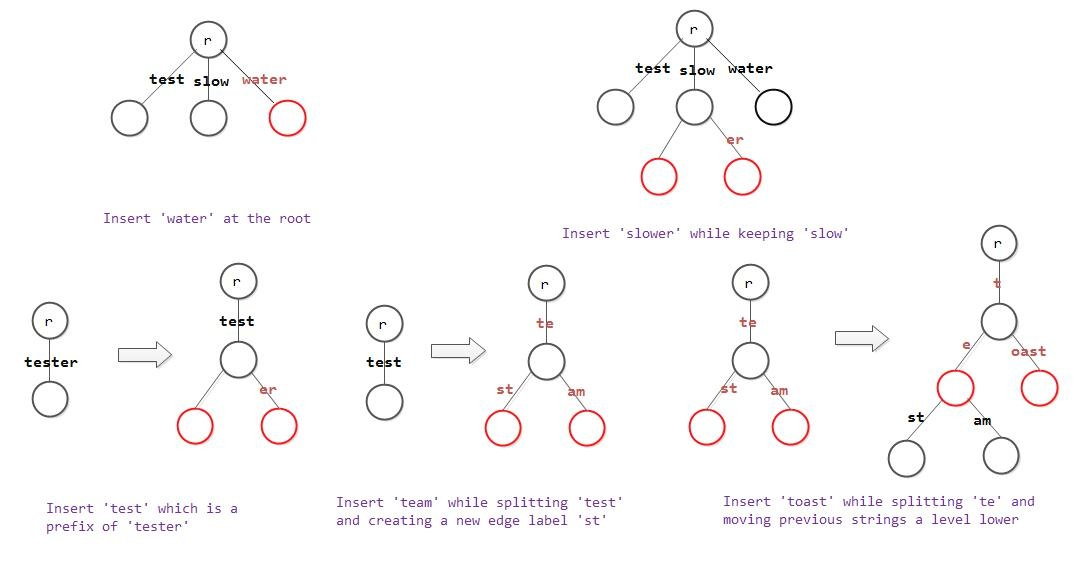
PATRICIA trie及其变体

PATRICIA trie，是一种特殊的字典树，每个中间节点记录key之间公共前缀的位置。从此位置之后，key之间产生不同，根据接下来的不同字符，转到不同的子分支。

Critial Bit trie

从基数树的角度看，PATRICIA trie最简单的一个实现是二进制的，即Critial Bit trie(cb trie)。critical bit的意思是两个串共同前缀分叉之处的比特。参见: https://cr.yp.to/critbit.html (这个作者对cb trie的吹捧，说实话有点过了)。

两种节点类型：

中间节点：存储critical-bit的位置，以及左右两个子树
叶子结点：存储整个串

构造流程（采用网上某个介绍进行了修改）：

        empty   -- initial state

---------------------------------------------------

       01234    -- number bit positions
insert 01011    -- the key


result root ----> 01011

---------------------------------------------------

insert 01010
    search ends at 01011~=01010;
    1st difference is at position 4, so...

result root ----> [4]    -- i.e. test position #4
                 .   .
               0.     .1
              .        .
           01010     01001

---------------------------------------------------

insert 10
    has no position #4;
    can skip key positions but must test in order, so...

result root ----> [0]    -- i.e. test position #0
                 .   .
               0.     .1
              .        .
           [4]          10
          .   .
        0.     .1
       .         .
     01010      01011

---------------------------------------------------

insert 000110;
    search ends at 01011~=000110;
    can skip key positions but must test in order, so...

result root ----> [0]
                 .   .
               0.     .1
              .        .
           [1]          10
          .   .
        0.     .1
       .         .
    000110       [4]
                .   .
              0.     .1
             .         .
            01010     01011

---------------------------------------------------

insert 01;
    01 is also a prefix of 01010 and 01011;
    must have ability to terminate at an intermediate node, as with Tries.
result root ----> [0]
                 .   .
               0.     .1
              .        .
           [1]          10
          .   .
        0.     .1
       .         .
    000110       [2] ---> 01
                  .
                 0.
                  .
                 [4]
                .   .
              0.      .1
             .          .
          01010        01011

quelques-bits popcount trie

为了减少cb trie的深度，采用4比特一组进行比较。即，基数树以2的4次方等于16为基数。二叉树->16叉树。同时，采用了位运算来压缩数组，减少了节点大小。quelques-bits popcount trie简写为QP Trie. 参见： https://dotat.at/prog/qp/README.html

构造过程和CB Trie类似：

insert keys:

"foo" -> hex str: "6 6 6 f 6 f"
"bar" -> hex str: "6 2 6 1 7 2"
"baz" -> hex str: "6 2 6 1 7 a"
"hax" -> hex str: "6 8 6 1 7 8"

result root ---->           [1]
                          .  .  .
                        2.  6.   8. ---> "hax"
                        .    .
                       [5]   . ---> "foo"
                      .   .
                    2.      .a
         "bar" <--- .         .---> "baz"

减少空间占用：用位图压缩子树数组

以此为例：
                            [1]
                          .  .  .
                        2.  6.   8. ---> "hax"

该节点保存有位图:
bitmap: 0000000101000100
index:  fedcba9876543210

正常情况我们需要一个大小为16的数组，其下标2、6、8分别指向对应的子数。
我们压缩子树数组为：
vector[3]
映射：
vector[0] -> '2'所在子树
vector[1] -> '6'所在子树
vector[2] -> '8'所在子树


查询算法：
设要查询i位置的子树，

mask = 1 << i;
if(bitmap & mask)
    member = vector[popcount(bitmap & mask-1)]

例如i = 8,

popcount(bitmap & mask - 1) = popcount(0000000101000100 & 0000000001111111)
= popcount(0000000001000100)
= 2

因此vector[2]就是'8'所在的子树

HAT trie

参见前面关于HAT trie的文章。

Adaptive Radix Tree

自适应的基数树。Adaptive Radix Tree。参见: https://db.in.tum.de/~leis/papers/ART.pdf

存在4种不同类型和大小的节点。根据实际某个节点的子树数量，自适应的改变node类型：

union Node {
    Node4* n4;
    Node16* n16;
    Node48* n48;
    Node256* n256;
}

关于其如何存储k-v，这里不作介绍。

Node4

因为子树数量较少，直接for循环比较查找子树：

    struct Node4 {
        char child_keys[4];
        Node* child_pointers[4];
    }

    Node* find_child(char c, Node4* node) {
        Node* ret = NULL;
        for (int i = 0; i < 4; ++i) {
            if (child_keys[i] == c) ret = node->child_pointers[i];
        }

        return ret;
    }

Node16

    struct Node16 {
        char child_keys[16];
        Node* child_pointers[16];
        byte num_children;
    }

可以采用SIMD进行并行加速查找：

    // Find the child in `node` that matches `c` by examining all child nodes, in parallel.
    Node* find_child(char c, Node16* node) {
        // key_vec is 16 repeated copies of the searched-for byte, one for every possible position
        // in child_keys that needs to be searched.
        __mm128i key_vec = _mm_set1_epi8(c);

        // Compare all child_keys to 'c' in parallel. Don't worry if some of the keys aren't valid,
        // we'll mask the results to only consider the valid ones below.
        __mm128i results = _mm_cmpeq_epi8(key_vec, node->child_keys);

        // Build a mask to select only the first node->num_children values from the comparison
        // (because the other values are meaningless)
        int mask = (1 << node->num_children) - 1;

        // Change the results of the comparison into a bitfield, masking off any invalid comparisons.
        int bitfield = _mm_movemask_epi8(results) & mask;

        // No match if there are no '1's in the bitfield.
        if (bitfield == 0) return NULL;

        // Find the index of the first '1' in the bitfield by counting the leading zeros.
        int idx = ctz(bitfield);

        return node->child_pointers[idx];
    }

Node48

    struct Node48 {
        // Indexed by the key value, i.e. the child pointer for 'f'
        // is at child_ptrs[child_ptr_indexes['f']]
        char child_ptr_indexes[256];

        Node* child_ptrs[48];
        char num_children;
    }

48个子树的数量，遍历等查找较慢，此时做了一个空间和查找速度的折中（可以对比Node256）。

    Node* find_child(char c, Node48* node) {
        int idx = node->child_ptr_indexes[c];
        if (idx == -1) return NULL;

        return node->child_ptrs[idx];
    }

Node256

这个就是最原始的做法

    struct Node256 {
        Node* child_ptrs[256];
    }

    Node* find_child(char c, Node256* node) {
        return child_ptrs[c];
    }

两种优化措施

两种优化：延迟展开、路径压缩，基本类似于最前面讲到的压缩字典树。

字典树的应用

字典树的应用也是非常广泛，这里举几个有代表性的例子，以后有时间会增加更多例子，以及对某些场景做进一步分析学习。

DNS(域名数据库、IP地址库)

DNS服务器中，通常有两个地方用到字典树：域名数据库和IP地址库。

互联网中的域名是一个层级结构的字符串，天生适合用字典树存储：

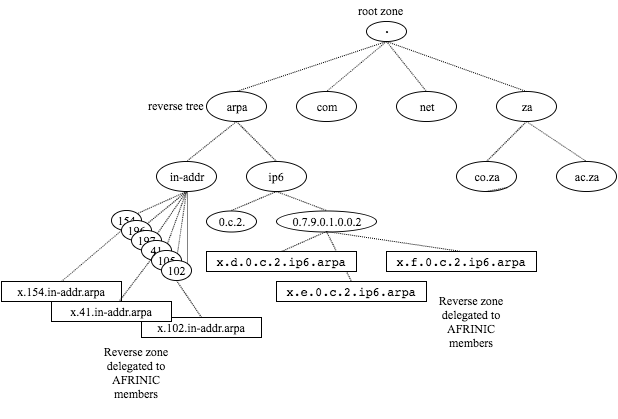
在Knot DNS Server中，采用了QP Trie作为域名的存储方案：https://github.com/CZ-NIC/knot/tree/master/src/contrib/qp-trie (早些时候的版本采用的是HAT trie)。

IP地址库，一般由许多条IP地址段(CIDR), 位置(地理区域，服务商)的记录组成。在权威DNS服务器中，用作EDNS进行基于地理位置的解析(geoip); 在Cache DNS中，用于缓存各权威服务的地址段。

在Knot中采用的QP trie实现了权威服务的geoip:(https://github.com/CZ-NIC/knot/blob/master/src/knot/modules/geoip/geoip.c) 、在Unbound中，采用类似CB trie做了EDNS缓存(https://github.com/NLnetLabs/unbound/blob/master/edns-subnet/addrtree.c)

路由表

路由表的存储、查找算法，经过持续不断的优化，目前可以说五花八门。由于路由表的特性，基于字典树的实现是其中有代表性的一大类。目前linux系统可以查看到按字典树组织路由表：

$ cat /proc/net/fib_trie
Main:
  +-- 0.0.0.0/0 3 0 5
     |-- 0.0.0.0
        /0 universe UNICAST
     +-- 127.0.0.0/8 2 0 2
        +-- 127.0.0.0/31 1 0 0
           |-- 127.0.0.0
              /32 link BROADCAST
              /8 host LOCAL
           |-- 127.0.0.1
              /32 host LOCAL
        |-- 127.255.255.255
           /32 link BROADCAST
     +-- 192.168.2.0/24 2 0 1
        |-- 192.168.2.0
           /32 link BROADCAST
           /24 link UNICAST
        |-- 192.168.2.110
           /32 host LOCAL
        |-- 192.168.2.255
           /32 link BROADCAST
Local:
  +-- 0.0.0.0/0 3 0 5
     |-- 0.0.0.0
        /0 universe UNICAST
     +-- 127.0.0.0/8 2 0 2
        +-- 127.0.0.0/31 1 0 0
           |-- 127.0.0.0
              /32 link BROADCAST
              /8 host LOCAL
           |-- 127.0.0.1
              /32 host LOCAL
        |-- 127.255.255.255
           /32 link BROADCAST
     +-- 192.168.2.0/24 2 0 1
        |-- 192.168.2.0
           /32 link BROADCAST
           /24 link UNICAST
        |-- 192.168.2.110
           /32 host LOCAL
        |-- 192.168.2.255
           /32 link BROADCAST

linux IDR

使用字典树，维护整数id到指针的映射。

IDR把每一个ID分级数据进行管理，每一级维护着ID的5位数据，这样就可以把IDR分为7级进行管理（5*7=35，维护的数据大于32位），如下所示：

31 30 | 29 28 27 26 25 | 24 23 22 21 20 | 19 18 17 16 15 | 14 13 12 11 10 | 9 8 7 6 5 | 4 3 2 1 0

例如数据ID为0B 10 11111 10011 00111 11001 100001 00001，寻址如下

第一级寻址 ary1[0b10]得到第二级地址ary2[]
ary3 = ary2[0b11111]
ary4 = ary3[0b10011]
ary5 = ary4[0b00111]
ary6 = ary5[0b11001]
ary7 = ary6[0b100001]
ary8 = ary7[0b00001]

酱猪蹄的博客