原文: https://tessil.github.io/2017/06/22/hat-trie.html

字典树 (也被称为前缀树) 是个有趣的怪物. 字典树是一种存储字符串的树形结构，一个节点的所有后代都共享相同的前缀. 这种结构可以进行快速的前缀查找, 例如查找所有以ap为前缀的单次, 并且由于共享前缀的特点，它可以采用紧凑的方式存储字符串.

跟大多数树形数据结构一样，前缀树的主流实现方法都存在缓存不友好的问题.在前缀节点之间遍历的每一步都可能会造成缓存缺失，这不利于进行快速查找。

本文中我们结合了传统字典树和缓存敏感哈希表，提出了缓存敏感的字典树：HAT-trie.

你可以从GitHub中找到 C++ 实现 ，以及一些HAT-trie同其他字典树和关联数据结构的 基准测试 .

接下来的章节, 我们首先更详细的介绍字典树的概念. 然后介绍 burst-trie 以及数组哈希表, 这些是HAT-trie所依赖的中间数据结构. 最后我们讲HAT-trie本身.

字典树

字典树是一种树， 每个节点拥有从 0 到 |Σ| 个子节点, 其中 |Σ| 表示字母表 Σ的大小. 对于简单的 ASCII 编码, 每个节点拥有总共 128 个子节点. 对于 UTF-8 编码， 我们可以把每个字符分割成 8比特编码单元， 然后每个节点对应存储每个编码单元，总共拥有 256 个子节点. 希腊字母 α 在 UTF-8编码中使用了两个八位单元, 0xCEB1, 可以存储到两个节点中, 一个子节点是 0xCE 八位员， 另一个子节点是 0xB1 八位元.

一个节点的全部后继节点共享该节点以及它的全部祖先节点作为字符串前缀.

没有后继的叶子节点，代表字符串结束。

接下来用图展示上面这些. 在示例中，我们会用到如下单词:

这些单词构成如下的字典树：

当我们想查找全部以roma开头的单词时，只需要向下遍历这棵树，直到找到所有的前缀字母。然后，我们只需要找出该节点的全部后继叶子节点，在本例中，我们将找出romane, romanes 和 romanus。

这样的结构实现起来就好象是k叉树一样。

为了存储孩子节点， 我们可以使用一个大小为 |Σ|(例如128, 在我们的例子中只需要支持 ASCII 编码)的数组。这样实现速度很快，但是内存利用率不高（使用稀疏数组/稀疏表可以减少内存消耗，当然也会变慢一点）。

class node {
    // array of 128 elements, null if there is no child for the ASCII letter.
    node* children[128]; 
};

在使用数组的情况下，有一种常见的减少内存占用的方法，叫做字母缩减技巧。我们使用一个包含 16 个字符 (4 比特)的字母表，替代包含256个字符(8比特)的字母表. 我们只需要把八位组切分成两个4位组 (4 比特) ，然后存为一对父子节点 (跟前文所述的 UTF-8 编码单元一样的方法). 更加紧凑，但是路径也会变长 (因此也会有更多潜在的缓存不命中).

另一种方案是简单的使用一个关联容器， 把一个字母编码单元映射到一个子节点. 如果我们想保持顺序，可以使用二叉搜索树或者有序数组, 否则使用哈希表. 速度更慢但是更紧凑，即使在字母表很大的情况下。

class node {
    // C++
    // Binary search tree
    std::map<char, node*> children;
    
    // Hash table
    // std::unordered_map<char, node*> children;
    
    // Sorted array
    // boost::flat_map<char, node*> children;
    
    
    // Java
    // Binary search tree
    // TreeMap<char, node> children;
    
    // Hash table
    // HashMap<char, node> children;
};

我们也可以把子节点存入一个链表. 父节点拥有一个指向第一个子节点的指针, 每个子节点有一个指针指向下一个节点 (它的兄弟). 这种情况需要做线性搜索来找到一个子节点. 紧凑，但是很慢.

class node {
    char symbol;
    node* first_child;
    node* next_sibiling;
};

注意 我们在图中用空节点作为可视化的标记, 来表示字符串的结束。在一个实际的字典树实现中，可以简单的在字符串末尾字符的节点里设置一个表示结尾的标记。

压缩字典树

减少节点大小非常重要, 但是我们也可以尝试减少节点数量，构建一个内存高效的字典树.

你可能注意到, 在前面画的字典树中, 一些节点构成了可以压缩的链表. 例如单词 rubicundus的结尾由 u -> n -> d -> u -> s 链接而成. 我们可以把这条链压缩成一个 undus 节点， 替代原先的5个节点.

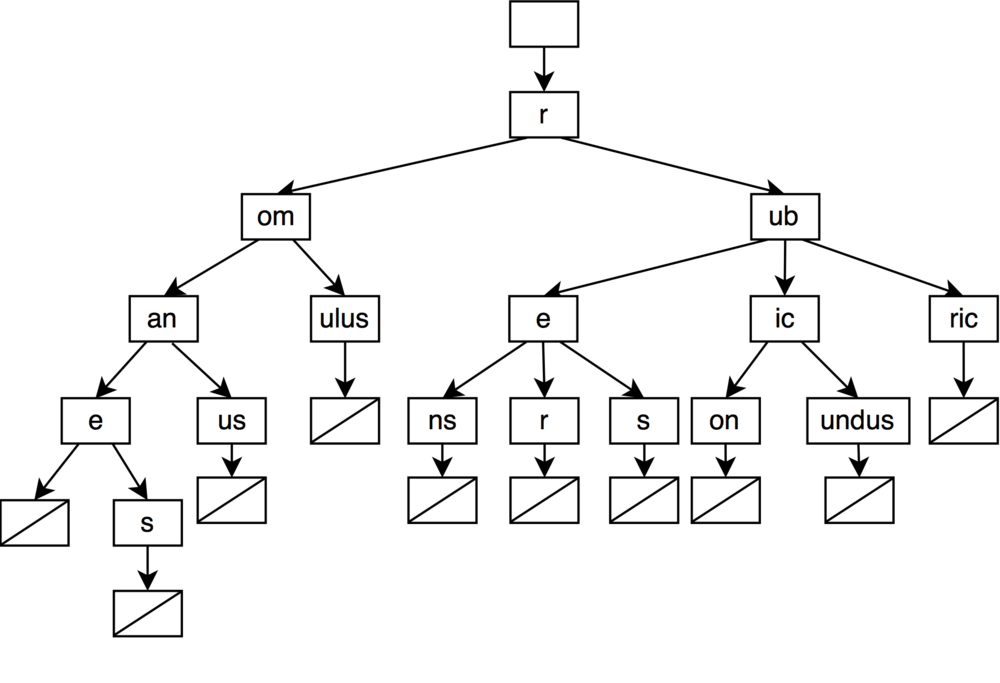
这种链压缩的思想已经被许多基于字典树的数据结构所应用. 鉴于篇幅原因，这里不对它们作详细介绍, 如果有兴趣可以参见 radix tries, crit-bit tries 和 qp tries.

我们已经了解了字典树的基本概念, 接下来进入到 burst-trie.

Burst-trie

Burst-trie 是一个类似于字典树的数据结构， 只不过字典树中叶子节点的位置被替换为一个容器，可以高效存储少量字符串. 内部节点是常规字典树的节点 (下图中我们用一个数组来表示指向子节点的指针).

容器本身可能存在各种各样的实现方式. 最初的论文研究了三种容器: 链表 (采用访问节点后移动到表头的访问方式), 二叉搜索树 和伸展树 (一种自平衡的二叉搜索树，频繁访问的节点会被移动到靠近树根的位置).

Burst-trie 由一个空容器作为初始， 随着新元素不断插入到字典树中而增长， 直到容器被爆裂启发(burst heuristic)判定为低效. 当这发生之时, 该容器会被爆裂为多个容器。

在容器节点爆裂的过程中, 会创建一个新的字典树节点，取代原先容器节点在字典树中的位置. 对于原先容器中的每一个字符串, 以其首字母作为新节点，除首字母外剩下的字符添加到新容器中，新容器作为新节点的子节点. 这个过程一直递归下去，直到全部新容器满足爆裂启发(burst heuristic).

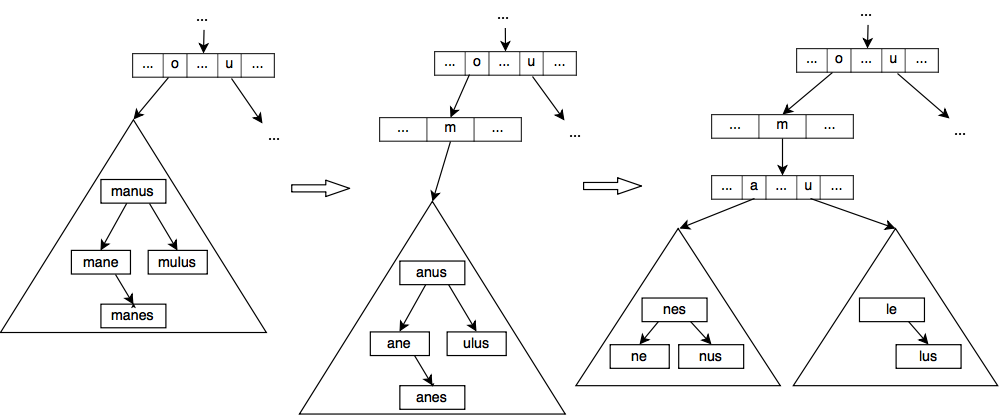
决定一个容器节点何时需要爆裂的爆裂启发方法有各种各样的实现方式. 最初的论文提出了三个选项.

• 限定. 最直接的方式是当容器中的元素数量大于预先定义的限制 L时，容器发生爆裂.

• 比率. 启发算法为每个容器节点设置两个计数器. 计数器 N 记录了容器被查询的次数, 计数器 S 命中容器中根节点的查询次数, 例如直接命中. 当比例 S/N 低于某个阈值, 容器会发生爆裂.

  当采用移向根节点的查询策略时，这种启发方法会很有用, 例如在伸展树中, 遇到不均匀的查询时 (一些字符串查询次数比另外的要多).

• 趋势. 容器创建时会分配一个资源量 C . 每次访问成功时, 资源量会被修改. 假如访问直接命中, 资源量增加 B, 否则资源量减少 M. 当资源量减少到 0 时，即发生爆裂.

  同比率启发一样, 当采用移向根节点的查询策略，并且遇到不均匀查询时，这种启发策略很有效.

数组哈希表

数组哈希表，是一种用来高效存储字符串的、缓存敏感的哈希表. 这是用来把 burst-trie 构建为 HAT-trie 的容器.

哈希表是一种平均查找时间复杂度为 O(1)的数据结构. 为了实现这种效果, 哈希表利用哈希函数把元素映射到一个桶数组中. 经过模运算，哈希函数把一个元素关联到桶数组的特定下标.

uint hash = hash_funct("romulus"); // string to uint function
uint bucket_index = hash % buckets_array_size; // [0, buckets_array_size)

问题在于，两个键可能会映射到同一个哈希桶 (例如， 当hash_funct("romulus") % 4 == hash_funct("romanus") % 4 时). 为了解决这个问题，所有的哈希表都实现了某种碰撞解决方案。

一种常见的做法是拉链. 桶数组中的每一个桶，都有一个包含该桶中全部元素的链表. 当插入元素的时候, 如果发生了碰撞, 新元素简单的追加到链表末尾.

关于哈希表的更多信息, 可以参考这篇维基百科的文章， 在此仅作简介.

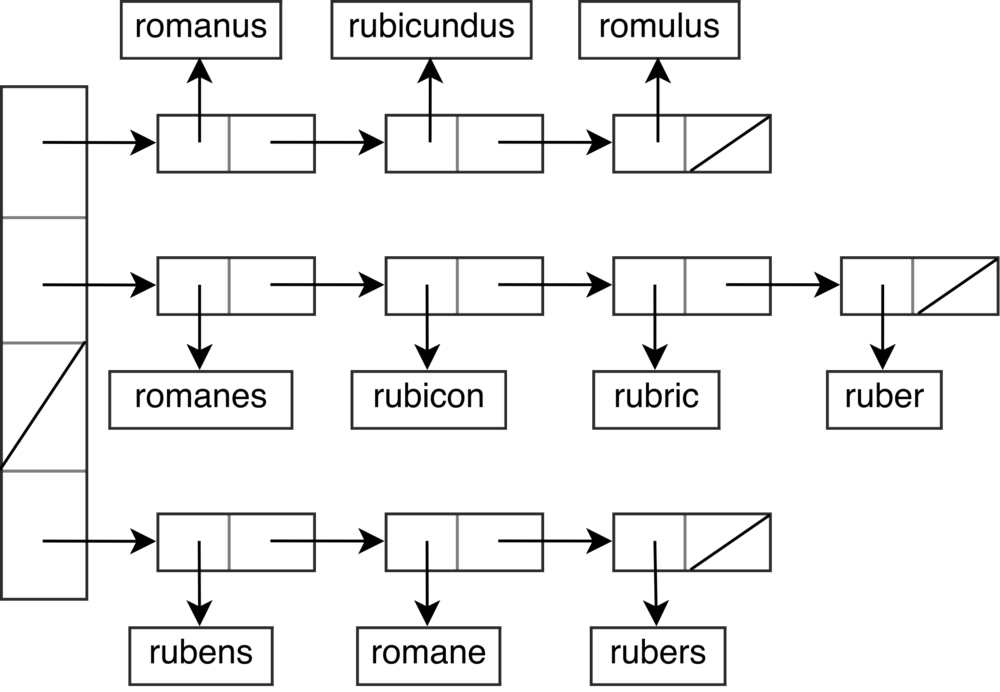
这种简单的拉链实现的主要问题在于缓存不友好. 在 C++ 中, 如果我们使用标准容器存储字符串, std::unordered_map<std::string, int>, 访问链表中的每个节点会导致两次指针解引用(如果实现采用了SSO短字符串优化，就只有一次解引用). 一次用来访问下一个节点，一次用来比较键是否相等.

除了潜在的缓存不命中之外, 这种方式要求一个节点至少存储两个指针 (一个指向下一个节点, 一个指向存储在堆中的字符串). 在字符串比较小的情况下，这会带来很大的开销.

数组哈希表的目标是，把一个桶中的所有字符串存储在数组而不是链表中，来减少上述这些不便之处. 这些字符串存储在数组中，使用他们各自的长度作为前缀. 大多数情况下, 我们在解决冲突时只会用到一次指针解引用 (如果数组很大的话会有多次解引用). 我们也不必存储多余的指针，从而减少哈希表的内存占用.

缺点是当一个字符串需要追加到桶中时, 可能会引起整个数组的内存重新分配.

数组哈希表提供了一种在哈希表中存储字符串的高效、紧凑的方法. 你可以在GitHub中找到HAT-trie使用的 C++ 实现.

HAT-trie

现在我们已经有了创建 HAT-trie 的全部材料, 接下来我们把这些全部组合在一起.

HAT-trie 是一种 burst-trie， 使用数组哈希表作为叶子节点的容器.

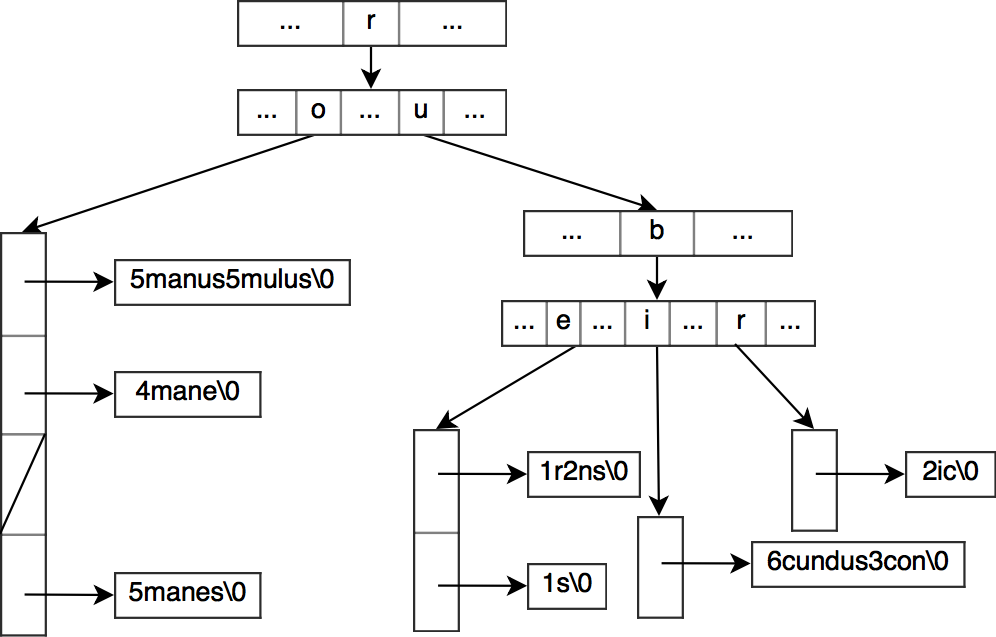
和 burst-trie 一样, HAT-trie 也使用一个空容器作为起始节点，这里用的是数组哈希表. 当容器节点变得过大, 就会开始爆裂过程 (HAT-trie采用了前文所述的限制爆裂启发策略).

本文提出了两种爆裂方案.

• 单纯. 采用类似于 burst-trie 的方式, 一个新的字典树节点被创建出来，占据了原先的容器节点. 原先容器中每个字符串的首字母被移除， 剩余的字符串被放入新建的数组哈希表中，数组哈希表作为新建字典树节点的子节点，每个新建的字典树节点对应到每个被移除首字母的字符串. 这个过程递归执行下去，直到新建的数组哈希表的大小不超出限制.

• 混合. 与单纯容器节点不同, 一个混合容器节点拥有超过一个的父节点. 当我们从一个单纯节点创建多个混合节点时, 我们需要寻找一个分隔字符， 它能尽可能平均的把单纯节点分为两部分. 所有首字母小于分隔字符的字符串进入左边的混合节点，其他的进入右边的混合节点. 然后，父节点会对小于分隔字符的字母设置指针指向左侧混合节点，剩下的指向右侧混合节点. 注意不同于单纯节点, 我们在容器中保留原字符串的首字母，以便于分别出来自哪个父节点.

如果我们爆裂一个混合节点, 我们不需要新建字典树节点. 我们只需要把混合节点分割为两个节点 (有可能成为单纯节点，如果分割后的节点只有一个父节点的话). 然后在父节点中重新分配子节点的指针.

采用混合节点可以帮助减少 HAT-trie 的大小.

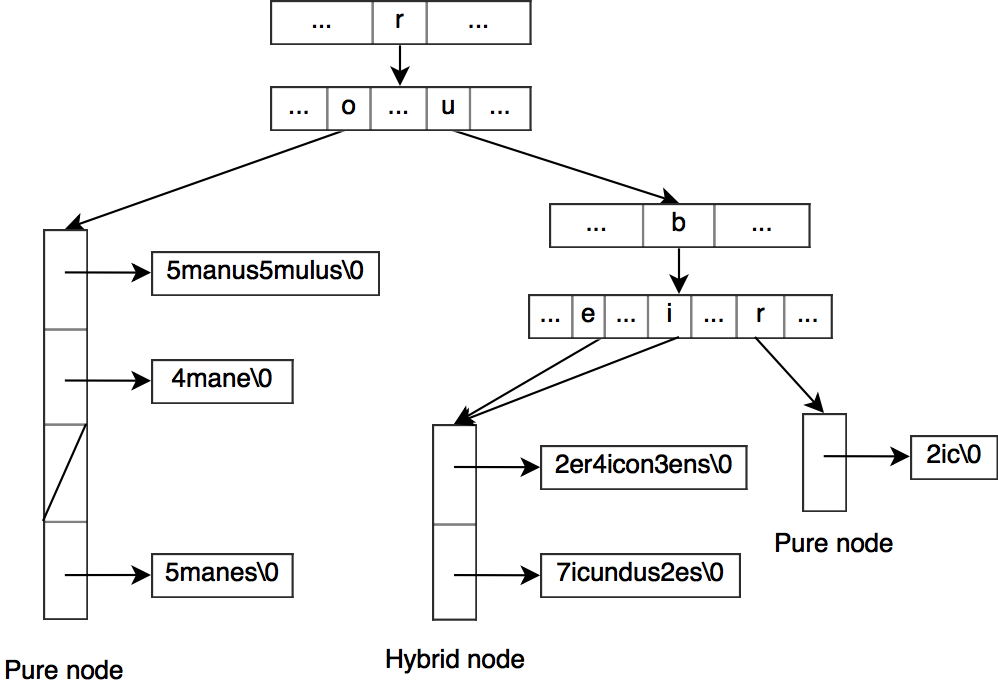
HAT-trie 的主要弊端在于元素只是一个近似有序的顺序，因为元素在数组哈希表中是无序排列的.

导致的结果就是在进行前缀查询时，我们可能需要做额外的工作，从数组哈希表中找到需要的元素.

如果我们查询全部以 ro 为前缀的单词, 事情比较简单，因为向下遍历树时，我们会到达一个字典树节点. 我们只需要返回该字典树节点下面的全部单词即可.

如果我们查询以 roma 为前缀的单词，事情就会变的复杂 。向下遍历时我们会到达一个容器节点，我们仍需以ma作为前缀进行进一步的查询. 这里不能保证容器节点中存在ma前缀 (例如 以mulus作为后缀的节点)，我们需要作一次线性查找. 但是由于数组哈希表的大小有上限, 前缀查询的时间复杂度依然是 O(k + M), 其中 k 是前缀的长度，M 是匹配该前缀的单词数, 即使在 HAT-trie 中存了千百万条数据. 我们只是拥有一个较高的常数因子，取决于数组哈希表的大小上限.

这种近似有序的另一个结果是，如果我们想在所有元素中进行顺序遍历, 当迭代器进入一个新的容器节点时，需要对容器节点的全部元素进行排序. 由于容器节点的大小上限是固定的, 也不会导致太差的结果, 不过在这种需要对元素排序的场景下采用其他数据结构可能更好一些。

最后，HAT-trie 在速度和内存占用方面取得了比较好的平衡, 你可以从基准测试 中看到, 在牺牲了元素有序性，转而采用近似有序的前提下.